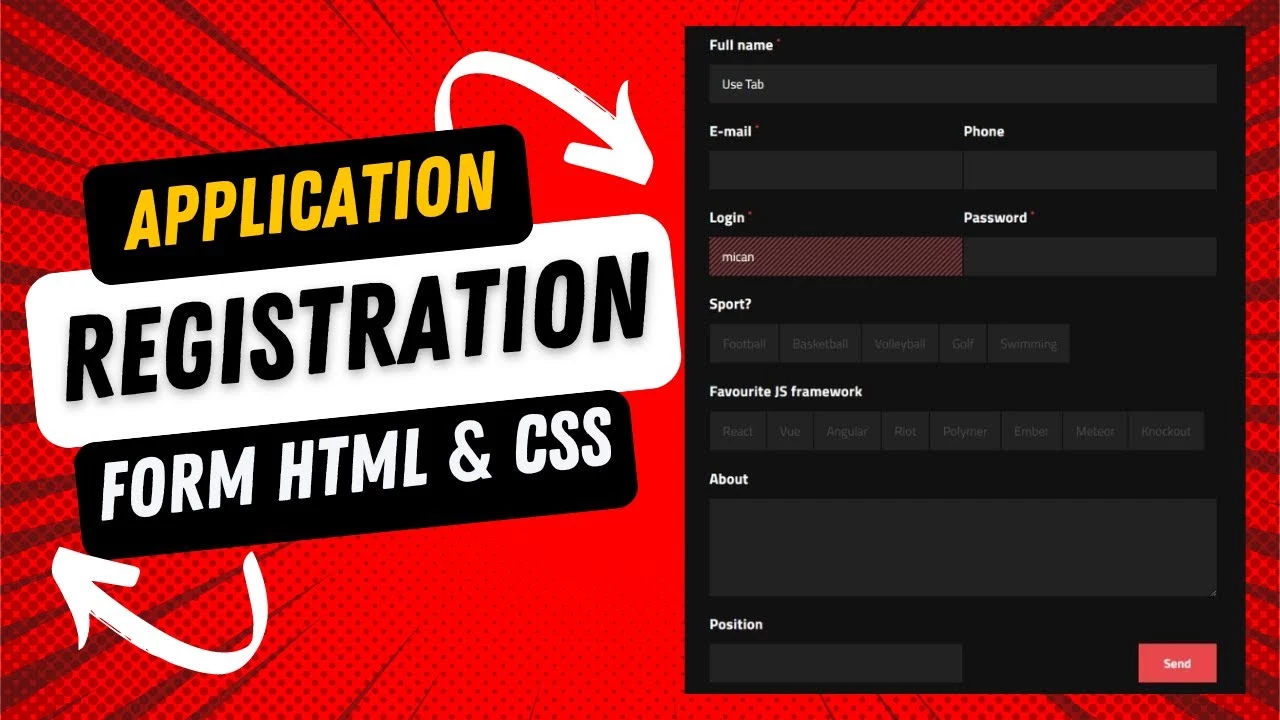
Registration form design is a very important part of website design. It is the first thing that a user sees when they visit your website. It is also the first impression they have of your company. Registration form design free download- Application form design – Registration form template HTML CSS JavaScript.
In this tutorial, we will take a look at how to create a responsive Registration form design. So make sure to check it out and follow the instructions to design a beautiful Registration form.
When it comes to registering for a job application, a user can be quite specific with the registration form they want to use. This is why they want a custom application form design. Here is a tutorial on how to create a responsive Registration form design.
Now we run into a problem, when moving from one subproblem to another we don’t know what our target amount is now. Initially the target amount is W
However, it will change every time you take a coin. We have to remember that somehow. The way to remember is to use another state. Then we redefine the function f(i,W)
Registration form design free download– Application form design – Registration form template HTML CSS JavaScript.
And again think about two options:
i
Using the th coin leaves us with a target of W–Ci. Then the next subproblem is f(i+1,W–Ci)
.
i
Not using th coin will not change our target. Then the next subproblem is f(i+1,W)
.
We need not take the minimum of two subproblems. In the first option, since we are taking coins, we need to add 1. Now write the formula:
Complexity:
Our subproblem number is n∗W
And each subproblem is doing the rest except calling other subproblems in constant time. The time complexity will be O(nW).
. (It’s not polynomial complexity, it’s pseudopolynomial, you can google it)
Iterative version:
We know that in the iterative version, table buildup starts from the subproblem being solved first. In our formula i
Its value goes forward from 0 and the value of W goes backward. We will start the table buildup from (n–1,0) cells. Then each subproblem is updated in topological order. If you have trouble understanding, my suggestion would be to manually update the cells one by one in a table of size n∗W.
I show it an arbitrary table in which corner the answer will be and in which direction the cells will update. Your task will be to update properly.
In iterative DP, you have to be careful about corner cases because instead of recursive function updating directly from the table, accessing the reverse index will give a runtime error. What I do here is put the table access code into a new function.
There is a great memory optimization opportunity here. Notice that in the inner loop we are only getting the values of i+1 rows. That means when the value of i is x then you only need the values of row x+1, the rest of the table is useless. That means the rest except the current row and the previous row are not working. Thus you are 2∗W
You can solve the problem by using the size table.
Variation:
Now we will see some variations of coin changer. Assume that our coin values are still the same C={2,5,9,13,15}
, but this time the supply of each coin is infinite. Earlier it took 3 coins to make 30 (15+13+2) but now it takes 2 coins (15+15).
.
This can be done by deleting only 1 character in the code. Think for yourself before reading the next line.
First if we take a coin the next state is f(i+1,W–C[i])
A was leaving, so a coin was not taken more than once. If we stay with the same coin after taking the ith coin, just update W only then it will work. The formula will now be:
The difference with the previous one is that I changed the first i+1 to i.
Now that we have some more optimization room, we can save space by reducing state if we want. Now that we have unlimited coins, we no longer have to worry about which coins we are taking. We can define the subproblem simply by f(W) if we wish. We want to find out how many coins it takes to make W, it doesn’t matter which coin I take now. Then run a loop inside the function and try to get coins one by one.
Now the time complexity is the same but the size of the table will be reduced a lot. A very common trick in dynamic programming is to reduce memory by using loops to minimize state.
Now a homework: What if each coin can be used at most k times?
Registration form design free download – Application form design – Registration form template HTML CSS JavaScript.
Dynamic Programming 4 (Longest Common Subsequence)
The problems we looked at had only 1 subproblem state. This time we will solve a slightly more complicated problem called Longest Common Subsequence or LCS. After learning this I will talk a little about the edit distance problem and it will be your job to solve it yourself.
In this problem you will be given two strings S
and W. You need to find the length of the longest common subsequence among them. Recalling the definition of subsequence, if you remove some characters from a string, what remains is the string’s subsequence. A string can have 2n subsequences. The image below shows two strings and their longest common subsequence.
Length of LCS is 3 in this case
.
Our problem is S
and LCS of W is to be found. We let the indices of S be i and the indices of W be j
I will publish with down now
Now we can think like this, initially we have the first index of the two strings i=0
and are at j=0 and we need to find lcs(0,0). Now if we can find lcs(i,j) for any (i,j) then we are done. lcs(i,j) denotes the LCS of suffixes S and W starting at i and jth index. eg lcs(1,2)
is the LCS of “ELLOM” and “RLL”.
Now when we (i,j)
3 things can happen when I am at:
S[i]=W[j]
, i.e. two strings have the same character. In that case, taking that character as part of LCS, we can find the LCS of the rest of the suffix. So now we have to solve the lcs(i+1,j+1) problem, no guessing here.
If S[i]≠W[j] the case is a bit more interesting. Since two characters do not match, we must discard at least one character. Now we have two choices, to calculate lcs(i+1,j) by discarding the ith index, or to calculate lcs(i,j+1) by discarding the jth index. You can understand that we will go to two paths and choose Max.
Getting i=n or j=m means we’ve gone to the end of a string, in which case 0
Must return.
We get our recursive formula then:
Now writing the code is very simple:
Complexity:
Our state is (i,j)
where i can have values in [0,n−1] and j can have values in [0,m–1]. Then there are n∗m total states and the remaining operations we did inside the recursion are the complexity constants. Then the total complexity will be O(n∗m), generalized to O(n2).
.
Iterative version:
To write the iterative version we need to understand the order in which the states are updated (topological order). Let’s take a look at the mem table:
In the recursive version this table is created after calling lcs(0,0) (the last row and column are not part of the table, shown for clarity). Each cell (i,j) in this table is updated either from its right corner cell (i+1,j+1) or from the cell above or below (i,+1,j), (i,j+1). So if you imagine each cell as a node in the graph it would look like this
It means that the lower right corner cell (n−1,m−1)
We have to fill the table starting from We can do it row by row if we want. Now my suggestion would be that for the above example you create the table once by hand, only then the thing will go into your head.
If we run a nested loop like this, we get the cells in topological order:
Iterative DP requires a little more care in handling base-cases. Life becomes a little easier if we start with the base-case on the table at the outset. The whole code would be like this:
A question to ponder before concluding. In some cases recursive function will work faster than iteration. Iterative DP always needs to fill up the entire table but recursive DP can return results in many cases without filling up the entire table. The question is why does this happen and for what kind of input will the recursive function work well?
Related Problem – Edit Distance
Two string S to you
, W is given. You can only perform 3 operations on S string, replace any character, delete any character, insert new character at any position. That means change, delete, insert are your 3 operations. Now your job is to replace the string S with W in the minimum operation
made up
For example, to make “blog” into “bogs” you can delete the l and insert the s at the end of the string.
Hints: Same as LCS with two indices i,j
Who should keep the state. Now you think what will be the change of i,j if you delete any character from string S. (Similarly find how i,j will change for the remaining 2 operations.)
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
All Links in Below:
Join Our FreeWebsiteCreate Facebook Group to get an instant update for projects, templates, design resources, and solutions.
Join Our YouTube Channel & Subscribe with Bell Icon for New Video:
Join Our Official Facebook Page For the Latest updates All Code Projects are Free:
Visit our service page to get premium services.
Free Website Create – HTML CSS, PHP, JavaScript Programming Projects For Free
Follow Us
Thank You,
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
FreeWebsiteCreate.net tries to provide HTML, CSS, SCSS, JavaScript, React, Android Studio, Java, PHP, Laravel, Python, Django, C#(C Sharp), and ASP.net-related projects 100% free. We try to make learning easier. Free Website Create always tries to give free projects to new learners. Free projects and source code will help to learn quickly.
They can save time and learn more. In this post, we share a free portfolio project website code with HTML and CSS. This free code portfolio contains a single landing page with a responsive design. In this post, we get a free best carpenter and craftsman service website designed by FreeWebsiteCreate with HTML, CSS, Bootstrap, and JavaScript.