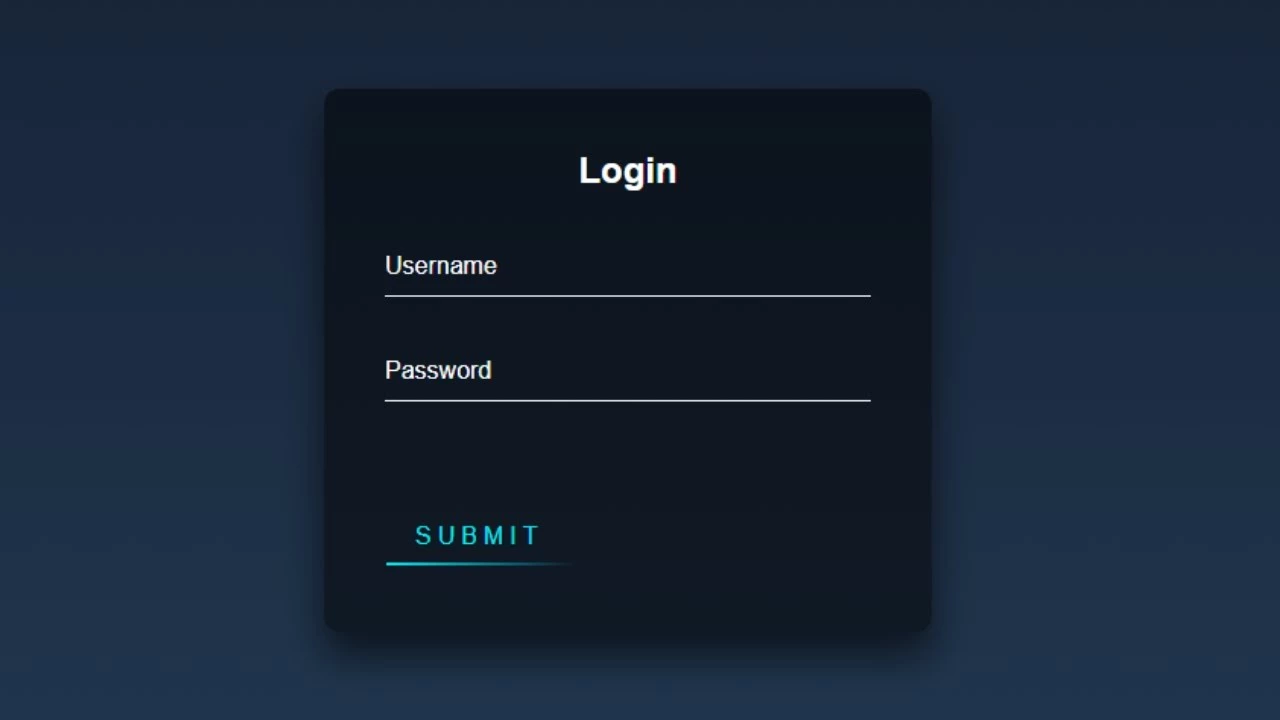
How to create an animated Login Form using HTML & CSS Coding tutorial. Creating an animated login form page with HTML, and CSS. This is also called a sign-in page design and you easily free download it from our website and also watch the full coding tutorial video for learning HTML CSS.
How to create an animated Login Form
Data structure: Binary indexed tree
Binary index tree is a very nice data structure and the best part is that the code can be written in minutes. And the downside is that it’s a bit difficult to understand what’s going on inside, but if you read carefully I’m sure there won’t be any problem. Another name of binary indexed tree or BIT is Fenwick tree. Before reading this article you should have a good knowledge of bitwise operations (AND,OR etc.).
We will learn about binary index trees to solve a simple problem. In this article we will assume that the index of the array starts from 1, after knowing how BIT works you will understand why it is important. You are given an array with 0 in each position. Now you will be given many operations. Each operation can be any of the following:
*i
Add the number x to the th index.
* 1 to i
Sum the sum of the subarrays at the th index.
In a very ‘naive’ way we get O(1)
Add x to each position and loop to get the sum in O(n). With BIT it is possible to get the sum in O(logn), but in that case the update operation is also O(log×n).
This must be done.
We know that every number can be written as the sum of some powers of 2. For example the binary of 13 is “1101”, binary has 1 in 0th, 2nd and 3rd positions. Then 13 can be written as 2^0+2^2+2^3 or 1+4+8. We will do some work using this property in binary index tree. Instead of adding the numbers to the array, we will do some work by writing the array indices as sums to powers of 2.
1
We can write the sum of the array from to i as the sum of some segments of the array. Suppose we have a function sum(i,j) whose task is to find the sum of all the elements of the array between index i and j. Then the sum for the 13th index would be sum(1,5)+sum(6,10)+sum(11,12)
. Here we have divided 13 into 3 segments. In binary index tree we divide each number into some segments. However, as we have done above, we will do it wisely. Since I will be using a “Binary Indexed Tree”, you can probably understand what to do using the binary representation of the indices of the array.
Since any number can be written as the sum of powers of 2, we can make 0 to subtract the power of 2 from the number. Subtracting 1, 4 and 8 one by one from 13 we get:
13-1=12
12-4 = 8
8-8 = 0
Then the segment for 13 will be sum(1,8)+sum(9,12)+sum(13,13)
. Another example will make it clear, 6(110 in binary)=2^1+2^2 can be written in the same way:
6-2=4
4-4=0
Now the segment for 6 will be sum(1,4)+sum(5,6)
.
Now you don’t need to worry about how to code, just think about whether you understand how division is done mathematically. Now we will see the segments in the image:
The segment is marked for 1 in the image. Next we will do for 2. 2 can be written as above:
2-2=0
So the segment will be from 1 to 2.
Now your job is to segment all the numbers up to 16 like this. Understanding how segments are created is the most useful part of binary indexed trees, so read it again if you don’t understand. Match the image below with your size:
By looking at this picture we can tell the segments for each number. For example, the segments for 11 would be (11,11),(10,9),(8,1).
. If you understand the above picture, then you understand how to find the segment by looking at the picture.
We already sum(i,j)
function defined. But using that function requires us to loop from i to j to get the sum we don’t want. We will define another array Tree[]. As you can see in the image each index of the array covers a subarray. For example index 12 covers the subarray (8,12). We will try to make Tree[i] contain the sum of the subarrays covered by the ith index. Then sum(8,12) will be saved in Tree[12], and sum(13,14) will be saved in Tree[14].
.
If I can do this then sum(11,11)+sum(10,9)+sum(8,1) for index 11
Without extracting we get tree[11]+tree[10]+tree[8]
I will get the sum only if I find out.
Now suppose I am called x at index 5
want to add I now need to intelligently add the number x to some index in the Tree array. We first add x to Tree[5] , then to the smallest index that covers 5 in the image above. That index is 6, so I will add x to tree[6]. Then 6 covers 8, so we add x to tree[8]. Then add x to tree[16] in the same way.
We will add x to the indices indicated by the arrow in the image in the tree array. The point to note here is that you can access maximum any of these 3 indices while calculating the sum in the above method. For example, if you access 16, you have to skip 5, 8, etc. and go directly to 1. Due to this property it is not possible to multiply the same update twice. To check if you understand the update operation correctly, put the arrow as above for 9 and then compare it with the solution below:
Starting from 9 in the image, each time I went to an index that completely covers the previous index. It is never possible to access more than one of these 4 indexes while calculating the sum!
Now we move on to the code. First we will implement the query operation. If a number is a power of 2, its binary representation is 1, 10,100,1000,100..00, ie some zeros after 1. Now I want to query for index number 11. 11 can be written as 1011 in binary. We first find the rightmost 1 and subtract the remainder from that position from the original number. Then minus 1 at the beginning.
1011-1=1010 (or 11-1=10 in decimal system)
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
All Links in Below:
Join Our FreeWebsiteCreate Facebook Group to get an instant update for projects, templates, design resources, and solutions.
Join Our YouTube Channel & Subscribe with Bell Icon for New Video:
Join Our Official Facebook Page For the Latest updates All Code Projects are Free:
Visit our service page to get premium services.
Free Website Create – HTML CSS, PHP, JavaScript Programming Projects For Free
Follow Us
Thank You,
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
FreeWebsiteCreate.net tries to provide HTML, CSS, SCSS, JavaScript, React, Android Studio, Java, PHP, Laravel, Python, Django, C#(C Sharp), and ASP.net-related projects 100% free. We try to make learning easier. Free Website Create always tries to give free projects to new learners. Free projects and source code will help to learn quickly.
They can save time and learn more. In this post, we share a free portfolio project website code with HTML and CSS. This free code portfolio contains a single landing page with a responsive design. In this post, we get a free best carpenter and craftsman service website designed by FreeWebsiteCreate with HTML, CSS, Bootstrap, and JavaScript.