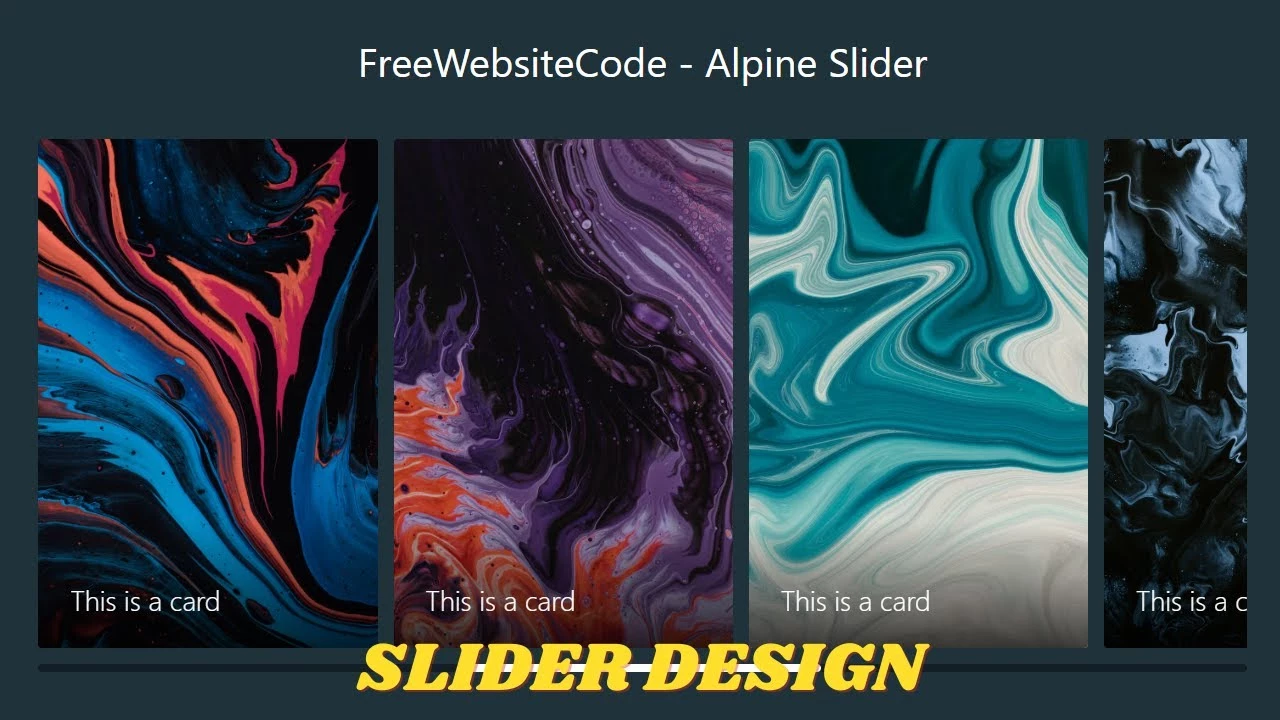
The slider is a very popular HTML, CSS, and JavaScript template. This is the perfect template for anyone who wants to create a slide-show site. It is also great for those who just want to create a simple site without any complicated coding. How to make a Slider – Alpine Slider – Slider Template HTML CSS JavaScript
It has everything you need to create your own site without having to worry about complicated code. The slider will automatically change slides when you click on the next button. The slider also has a built-in image gallery that allows you to upload your images and display them on the slide show.
How to make a Slider – Alpine Slider – Slider Template HTML CSS JavaScript
Binary Search – 1
You must have noticed that even though there are millions of words in the dictionary, it never takes much time to find the required word. This is because words are arranged alphabetically.
So if you try to look up the word dynamite in the dictionary and randomly turn to a page and find the word kite, you can be sure that the word you’re looking for is somewhere on the left. Again, if you find the word dear, then you will not try to search the pages on the left. In this way any word can be found in the dictionary in a short time.
Binary search is one such method that can be used to find any information from an array.
Suppose you have an array of numbers like this:
100,2,10,50,20,500,100,150,200,1000,100
Since the numbers are arranged randomly, it is not easy to find a specific number from here. If you want to find the number 500 from the array then you have to check all the indexes, it is called linear search. If the size of the array is n
Then the time complexity of linear search is O(n).
How to make a Slider – Alpine Slider – Slider Template HTML CSS JavaScript
But finding becomes much easier if the numbers are arranged as follows:
2,10,20,50,100,100,100,150,200,500,1000
Now if we have to find the number 150 then we will first check the exact middle index. If the first index is 0 and the last index is 10, the middle index is (0+10)/2 or the 5th index.
$2, 10, 20, 50, 100, 100, 100, 150, 200, 500, 1000
The middle index number is 100 which is less than 150, we know that the number is somewhere on the right side, we don’t need the left part anymore.
100, 150, 200, 500, 1000
Now I will do the same again with the remaining part. Now the middle index number is 200 which is greater than 150. That means we can throw away the right part.
100, 150
Now the middle number is 100 which is smaller than 150. Again I will drop the left part, there will be only:
150
Now the middle index number is 150. That means the desired number has been found.
In binary search we discard exactly half of the array each time and search the other half. A number is n
What is the maximum number of times that can be divided by 2 till the number becomes 1? The answer is log2n. So after at most log2(n) number of steps in binary search we will find the desired number, complexity O(log2n)
.
But one problem is that before doing the binary search, the numbers must be sorted from smallest to largest or largest to smallest, this process is called sorting. An array is O(n×log2n) no matter how hard you try.
Less complexity cannot be sorted.* Then one can say that we can find the number by linear search in much less time than the time it takes to sort, why do binary search? If you need to search an array only 1 time, then linear search is much better than binary search by laboriously sorting. But what if an array needs to be searched many times? As in a dictionary where different words need to be looked up at different times, it is wise to sort.
If we input 100 in the above code, it will return 5, because after sorting the array, there is 100 at index 5. But looking at the sorted array we see that 4,5,6 all have 100 at their index. If we want to return the leftmost index if a number occurs more than once, how should we change the code? In that case the binary search function would be:
Only 1 line has been changed, now after finding a number I will continue to search the rest of the left without stopping the search.
Lower bound: You are given a sorted array. You are a new number X
want to insert into that array. The lower bound is the leftmost index at which the array will still be sorted if you insert the number and move the rest of the numbers to the right. Think of the array as:
10 20 20 30 30 40 50
Then the lower bound of 20 is index 1 (0 based index), because the array remains sorted even after you put the number 20 at index 1 and move the rest of the numbers to the right. As such, the lower bound for 25 is index 3.
In simple words, the leftmost index that has a number equal to or greater than X is the lower bound. X
If every number in the array is greater than then the index after the last index i.e. the nth index is the lower bound where n
is the size of the array.
In the following code, the lower index is found by binary search, then the new number is placed in that index.
(It takes O(n) time to insert numbers in array like this. Using linked list instead of array can be inserted in O(1) time but in that case binary search is not possible because any index in linked list cannot be accessed randomly, it has to be accessed by pointer. One way would be to organize the data in the form of a binary search tree, which we will not cover in this article, you can learn it yourself if you want.)
Upper Bound: The upper bound is the rightmost index at which the array will be sorted when you insert the new number. That means the leftmost index that has a large number of X is the upper bound. In the example above, the upper bound of 20 is index 3. The code to find the upper bound remains as your homework!
The first episode ends here. In the next episode, I will discuss the bisection method.
* O(n) using counting sort or radix sort
Sorting can be done, but they only work on certain types of input. It can be mathematically proven that sorting is not possible in less than O(log2n) if there is no condition on the type of the input.
Happy Coding!
How to make a Slider – Alpine Slider – Slider Template HTML CSS JavaScript
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
All Links in Below:
Join Our FreeWebsiteCreate Facebook Group to get an instant update for projects, templates, design resources, and solutions.
Join Our YouTube Channel & Subscribe with Bell Icon for New Video:
Join Our Official Facebook Page For the Latest updates All Code Projects are Free:
Visit our service page to get premium services.
Free Website Create – HTML CSS, PHP, JavaScript Programming Projects For Free
Follow Us
Thank You,
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
FreeWebsiteCreate.net tries to provide HTML, CSS, SCSS, JavaScript, React, Android Studio, Java, PHP, Laravel, Python, Django, C#(C Sharp), and ASP.net-related projects 100% free. We try to make learning easier. Free Website Create always tries to give free projects to those who are new learners. Free projects and source code will help to learn easily. They can save time and learn more. In this post, we share a free portfolio project website code with HTML and CSS. This free code portfolio contains a single landing page with a responsive design. In this post, we get a free best carpenter and craftsman service website designed by FreeWebsiteCreate with HTML, CSS, Bootstrap, and JavaScript.