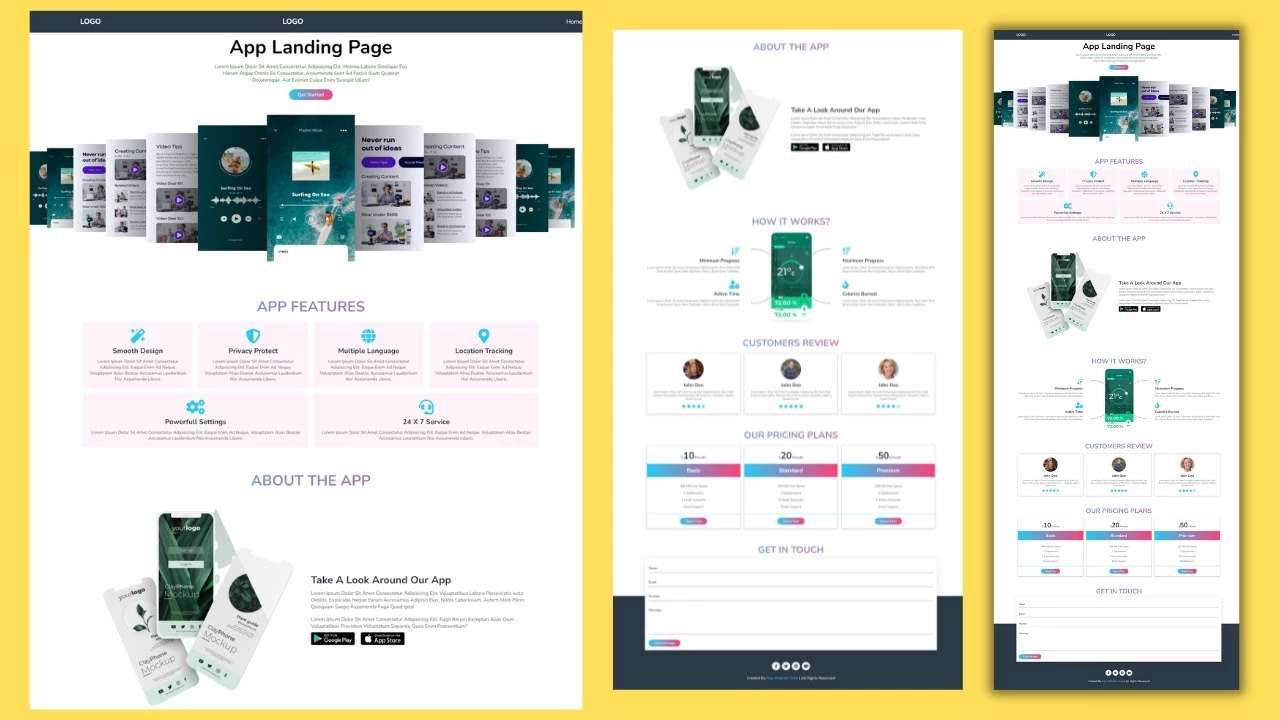
How to make an App Landing Page Template – Free Landing Page Templates – Web Design – Get 100% Free
A Completely responsive mobile app website landing template with HTML, CSS, Bootstrap, and JavaScript. This is also called app landing page website design and you easily free download it.
Landing pages are the best way to generate sales for your business. They allow you to showcase the value of your product or service and provide an easy-to-navigate way for potential customers to make a purchase. Landing pages also help you convert visitors into leads and customers.
The more leads you to have, the more money you make. And the best part is, that a landing page is not just for your website or app. They are also perfect for a mobile app. In this article, we will look at some of the best mobile app landing page templates that you can use to increase the number of leads you receive and sell more products.
Meet in the Middle Technique
Meet in the middle is a very elegant problem-solving technique. Its task is to solve the problem by dividing the problem into two parts and then merging the two parts in some way. But the difference with Divide and Conquer is that in Divide and Conquer, after dividing into two parts, the small parts are divided repeatedly, in Meet in the Middle we will divide only once.
How to make an App Landing Page Template – Free Landing Page Templates – Web Design – Get 100% Free
We will look at some of the problems that can be solved with Meet in the Middle.
Problem 1: Sum of Four
(Required Knowledge: Binary Search)
4 o’clock n you
Given an array of size A,B,C,D. Select exactly one value from each array such that their sum is 0.
ie 1+ if n=3 and A={1,2,3}, B={−1,−4,−5}, C={1,5,8}, D={9,8,5} (−4)+8−5=0
Maybe a solution.
Solution-1
The first solution that comes to mind is to run 4 nested loops and add the numbers in all combinations. Its complexity will be O(n4).
. If n=1000
Otherwise, the program will take several hours to complete.
We have 4 values a,b,c,d
Required so that a+b+c+d=0. It can be written, (a+b)=−(c+d)
. a will get the value from the A array, b will get the B array, c will get the C from the array and d will get from the D array.
Now execute two nested loops to find out all possible combinations of A and B arrays. Then we get all (a+b). Sort all values or insert them into a map.
Again run two nested loops to find all possible combinations with C and D arrays. Now got all c+d. Find a+b for each c+d by performing a binary search on the previously sorted value or by searching through the map.
Now our complexity is O(n2∗logn2)
. If the values are small then use simple boolean flags instead of map O(n2)
This can be solved.
Problem 2: Coin Change
(Required knowledge: All subset generation using binary search, backtracking or bitmask)
Suppose you have some coins. It should be said that a certain value can be created by using some coins from them. No coin can be used more than once. For example if the coins are 1,3,6,10 then you can make 13 or 11 but not 50 or 2 at all. Maximum number of coins is 30.
solution
I think the value of the coins can be from 1 to 100. If you know dynamic programming then you must be thinking that it is a very simple problem, the sum of the value of all the coins can be maximum 30*100, then the problem can be solved very easily in 30*(30*100) complexity.
Now I make the problem harder, suppose the values of the coins can be from 1 to 10^9. Now the complexity is 30*(30*10^9). It is possible to solve it with dynamic programming, no memory or time will be wasted. What can be done now? Note that the number of coins is very low!
Even if the number of coins is only 30, the number of subsets of a set of 30 coins is 2^30. That means a maximum of 2^30 different values can be created with the coins. So it is not possible to generate all the values by backtracking.
But if there were 15 coins then there would be 2^15=32768 subsets and we could generate all the values by backtracking! After reading so far, stop for a while and think about how to solve the problem. Then read the following section.
We divide the coins into two parts. Each part has 15 coins. Now take the 15 coins of the first part and generate all the values and put them in an array, I think the name of the array is A. Similarly take the 2nd 15 coins and generate all the values and put them in another array, I think the name of the array is B. Sort the B array, A doesn’t need to be sorted.
Now the rest is easy. Suppose you have to make the X value. Loop over array A and check all values. If the ith value is A[i] then you check if the array B contains the value X-A[i]. If yes then you can make X!! B You have sorted, then you can check if X-A[i] exists by binary search. If you think about it, you will realize that array A contains all combinations of the first 15, so there is no need to look for X-A[i] in A.
For n coins then the complexity will be O(2(n/2)*log2(n/2)), because we are doing a binary search on the other half for 2(n/2) values.
Problem 3: Bidirectional search
(Required Knowledge: Graph Theory)
Given two nodes in a graph, find the shortest path between the two nodes.
Solution:
Pretty sure those who know graph theory are scratching their heads, is this a problem? Can be solved with BFS. But here we are thinking about huge graphs that may have billions of nodes and edges.
How to make an App Landing Page Template – Free Landing Page Templates – Web Design – Get 100% Free
In BFS, each node has to travel to its adjacent nodes, and from them to its adjacent nodes. The number of adjacent nodes of each node is called the node degree. Now if the average degree of each node is p and the shortest path is k then you need to explore the node in roughly O(pk).
If you start the search from both the source and destination sides until they match then the complexity becomes O(pk/2). As you can see from solving the previous coin change problem, this halving is a very significant improvement in an exponential complexity.
Two other interesting problems related to roughness are:
1. Find out whether two users have mutual friends in the Facebook graph
2. It is assumed that the distance between any two people in the social network is maximum 6 nodes. How to verify if you input two usernames?
Reference: Info Arena
Acknowledgment: Thanks to Mahbubul Hasan Shanto Bhai for pointing out the error in the solution of the sum of four problems.
Problem to solve:
Coin Change(IV)
Sum of Four
Funny Knapsack
Happy Coding!
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
All Links in Below:
Join Our FreeWebsiteCreate Facebook Group to get an instant update for projects, templates, design resources, and solutions.
Join Our YouTube Channel & Subscribe with Bell Icon for New Video:
Join Our Official Facebook Page For the Latest updates All Code Projects are Free:
Visit our service page to get premium services.
Free Website Create – HTML CSS, PHP, JavaScript Programming Projects For Free
Follow Us
Thank You,
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
FreeWebsiteCreate.net tries to provide HTML, CSS, SCSS, JavaScript, React, Android Studio, Java, PHP, Laravel, Python, Django, C#(C Sharp), and ASP.net-related projects 100% free. We try to make learning easier. Free Website Create always tries to give free projects to new learners. Free projects and source code will help to learn quickly.
They can save time and learn more. In this post, we share a free portfolio project website code with HTML and CSS. This free code portfolio contains a single landing page with a responsive design. In this post, we get a free best carpenter and craftsman service website designed by FreeWebsiteCreate with HTML, CSS, Bootstrap, and JavaScript.