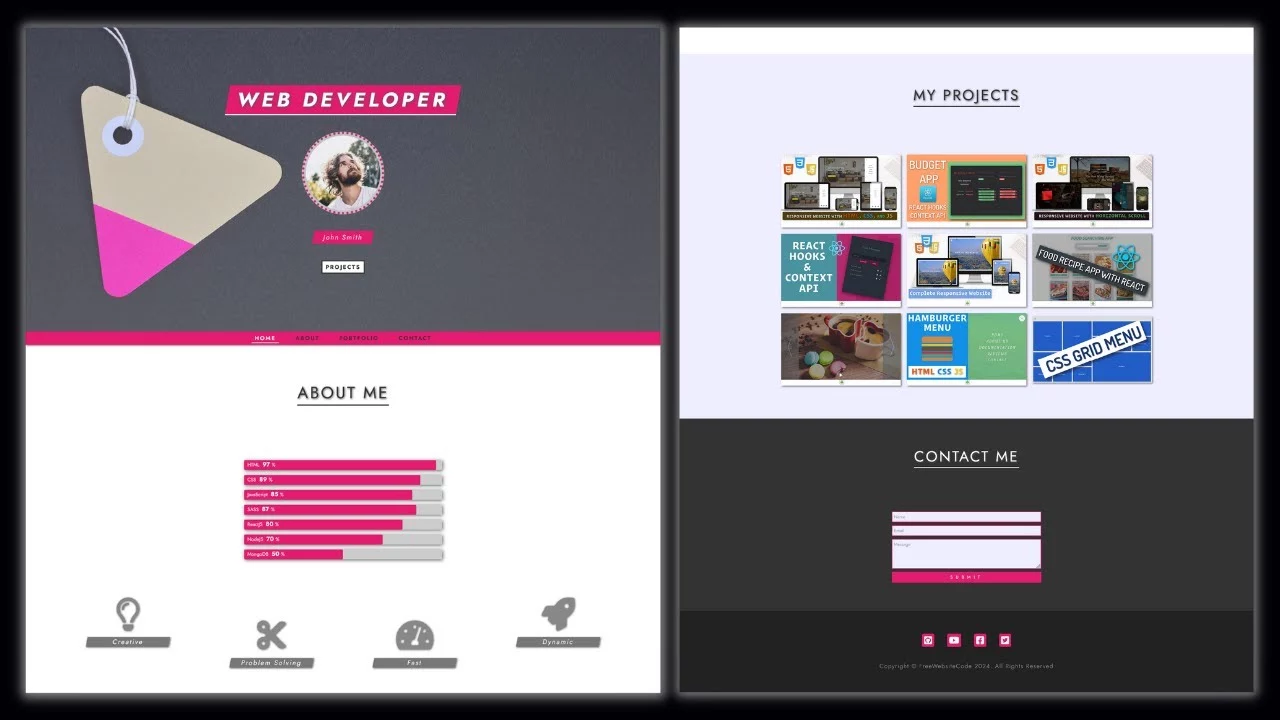
This is a portfolio website focused on HTML CSS coding, which can be used as a personal portfolio website. The youtube video tutorial will go over how to create a responsive personal portfolio website. Responsive Web Developer Portfolio – Personal Portfolio Website Design HTML CSS JavaScript
The tutorial is targeted at developers who want to learn more about designing websites using HTML CSS coding. People with a personal website will showcase their skill works portfolio.
Longest path problem
You are given an unweighted graph and a source node. You need to find the maximum length path from the source node. This is the longest path problem. The question is how to solve the problem?
This is one of my favorite interview questions. So far in about 7-8 interviews I have asked this question, only 2 answered it easily, 1 after giving hints, all the rest answered wrongly. Many people get A+ in Algorithm course, but this kind of question shows how much the candidate really knows.
The first mistake everyone makes after asking the question is not asking what is the definition of the maximum length path, I can make the length infinite by going back and forth between two nodes an infinite number of times. So a better definition of longest path is needed to solve. Let’s say I want a longest path where no node is visited more than once. Now there is no chance of the length being infinite.
Figure shows the maximum length path from node 1 which is 4 (1->2->5->4->6).
Before thinking about the solution, the next question is whether the graph is directed or undirected. Assume the graph is undirected and can have at most 100,000 nodes.
Responsive Web Developer Portfolio – Personal Portfolio Website Design HTML CSS JavaScript
I have seen candidates give many wrong solutions to this problem, such as:
KO attempts to find the shortest path by taking the weight-1 of the edges of the KO graph. It won’t work either way, stuck in an infinity loop.
Anyone who tries to solve this using dynamic programming will also not work and will get stuck in a loop.
Many people want to use Max Flow but that will not work either.
So what is the solution? Let the grafter node number be n
. Since the value of n can be very large, a polynomial solution is required. Now consider a graph in which the length of the longest path from the source is n−1. Like the graph below:
The length of the longest path in this graph is n−1 where n=6
. That is, graphta has a source node from which all nodes can be traveled once without repeating any node. If you have studied a bit of graph theory, you should know that the Hamilton path problem is an NP-complete problem. So far no one knows of a way to solve an n-p complete problem in polynomial time.
As you can see the Hamilton path problem can easily be converted to the longest path problem. Find the longest path from a source in a graph such that the path length is n−1
, this is the Hamilton path problem. If the longest path problem could be solved in polynomial time, the Hamilton path problem would be solved too!
So we can see that the longest path problem has no polynomial solution. If the number of nodes is very small then it is possible to solve this problem by backtracking, but its complexity is exponential. The longest path is an n-p hard problem.
Now the question is why the Hamilton path problem is n-p complete but the longest path is n-p hard? If you don’t know the answer then read this article of mine.
Happy coding
Algorithm Game Theory 3 (Sprague-Grundy Numbers)
Now that we know how to solve the nim-game, we will now solve some composite games with Grundy numbers.
Consider a game where s
There is a pile of stones, each time a player can pick up 1 or 2 stones, the one who picks up the last stone wins. By looking at the number of stones you have to tell if the first player will win if played optimally. It is very easy for you to solve it if you have read the first part. Our sudocode will look like this:
Now suppose the number of stacks of stones is n instead of one and each stack has s1,s2……sn
There is stone. A player can pick up 1 or 2 stones from either stack, the last stone to be picked up wins. How to solve this time? Such games are called composite games.
We will assign a Grundy number to each stack. If the grandy number of a stack is g, we can assume that the stack is g in Nimgame
Responsive Web Developer Portfolio – Personal Portfolio Website Design HTML CSS JavaScript
It is equivalent to a pile of stones. For n stacks we get n Grundy numbers g[s1],g[s2]….g[sn], and then g[s1]⊕g[s2]⊕……..gn as nimgame.
We will know who will win the game.
The rule for finding the grandi number for each state is that the grandi number of the other states that can be reached from that step must be found first. Let their set be X={x1,x2,…}
. Now the lowest number not in this set will be the grandi number of the current state. An example will make it clear.
Suppose there are 0 stones in a pile. Our state is s=0
. As we know this is a losing position, we can assume that for s=0 the Grundy number g[0]=0
.
If pile contains 1 stone then s=1
. From here 1 stone can be moved to state s=0. The set X then has X={g[0]}={0}. 1 is the smallest number not in X, so we assume g[1]=1
.
If there are 2 stones in pile then s=2
. From here 1 or 2 stones can be moved to s=1 or s=0 state. The set X then has X={g[1],g[0]}={0,1}. 2 is the least number not in X, so we assume g[2]=2
.
If there are 2 stones in pile then s=2. From here 1 or 2 stones can be moved to s=1 or s=0 state. The set X then has X={g[1],g[0]}={0,1}. 2 is the least number not in X, so we assume g[2]=2
.
If there are 3 stones in pile then s=3
. From here 1 or 2 stones can be moved to s=2 or s=1 state. The set X then has X={g[2],g[1]}={2,1}. 0 is the smallest number not in X, so we assume g[3]=0
.
Doing the same calculation you get g[4]=1
, g[5]=2
etc.
Now if 3 stacks {5,2,3}
If there are stones then you can say that the game {g[5],g[2],g[3]}={2,2,0} is equivalent to playing the normal Nim game with stones. Now you are xorsum
You can tell who will win the game.
A simple pseudocode for finding Grundy numbers might be:
If you have understood so far then solve the following problem:
k on a chess board
There are coins. If a coin is in the (x,y) cell, the coin is moved to (x-2, y+1) or (x-2, y-1) or (x-1, y-2) or (x+1, y-2) per move. ) can be moved into the house, but the coin cannot be moved out of the board.
In each move the current player can move one coin according to the above rules. The player who cannot move the coin loses. You will be given the coordinates of the coins to predict who will win the game.
If you calculate the Grundy number for each square on this chess board, you get a table like the one below:
Notice that the grandi number of the houses from which no other house can be reached is 0, that means those houses are losing positions. To calculate the Grandi number for the rest of the rooms, first calculate the Grandi number of the rooms that can be reached from one room to another. Assume that the set of numbers is S. S is the smallest non-negative number
This will not be the grandiose number of the current house.
That’s it for today. Solve these problems if you understand how to calculate Grundy numbers. Try to figure out why this method works.
Happy Coding!
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
All Links in Below:
Join Our FreeWebsiteCreate Facebook Group to get an instant update for projects, templates, design resources, and solutions.
Join Our YouTube Channel & Subscribe with Bell Icon for New Video:
Join Our Official Facebook Page For the Latest updates All Code Projects are Free:
Visit our service page to get premium services.
Free Website Create – HTML CSS, PHP, JavaScript Programming Projects For Free
Follow Us
Thank You,
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
FreeWebsiteCreate.net tries to provide HTML, CSS, SCSS, JavaScript, React, Android Studio, Java, PHP, Laravel, Python, Django, C#(C Sharp), and ASP.net-related projects 100% free. We try to make learning easier. Free Website Create always tries to give free projects to those who are new learners. Free projects and source code will help to learn easily.
They can save time and learn more. In this post, we share a free portfolio project website code with HTML and CSS. This free code portfolio contains a single landing page with a responsive design. In this post, we get a free best carpenter and craftsman service website designed by FreeWebsiteCreate with HTML, CSS, Bootstrap, and JavaScript.