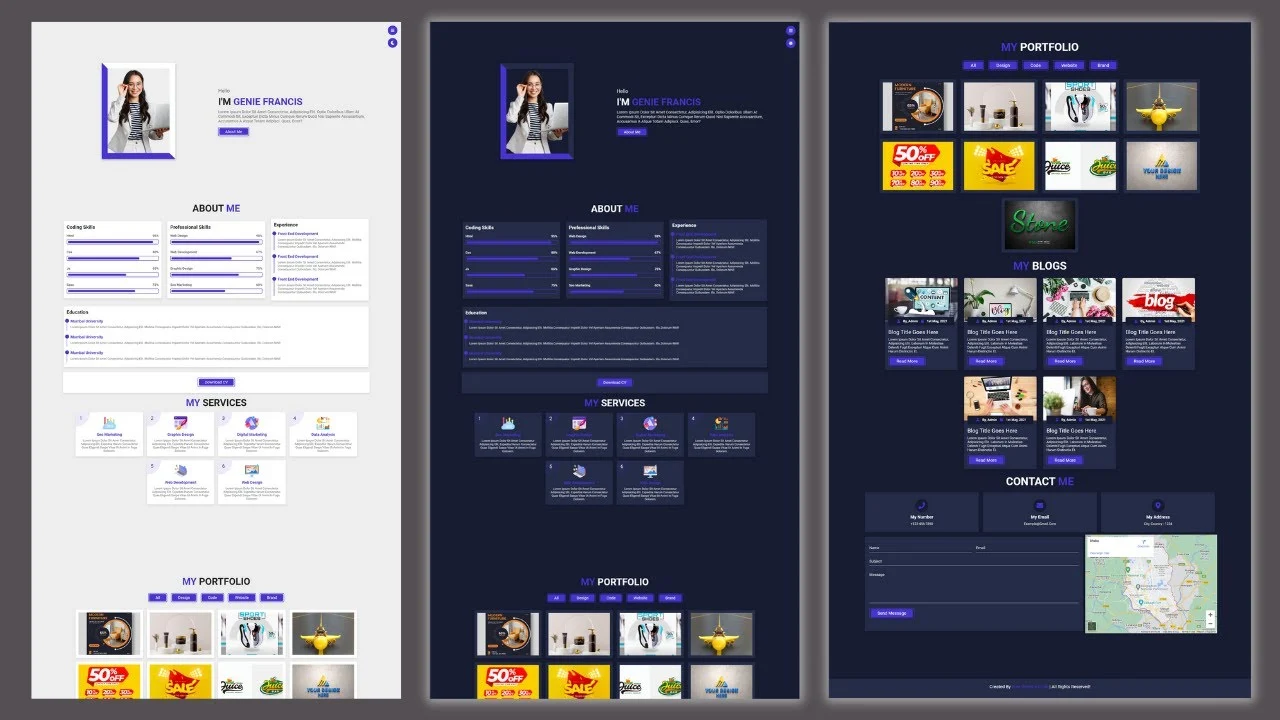
A Completely responsive portfolio website template with HTML, CSS, Bootstrap, and JavaScript. This is also called personal portfolio website template design and you easily free download it from our website free website create. Portfolio Website Template – Personal Portfolio Website Free Download HTML CSS JavaScript
Having a website is a great way for developers to showcase their skills and for prospective employers to get a good idea of what they are looking for. However, it can be difficult to create a website that is decent looking and easy to navigate. In this article, I want to share a free portfolio website template with you.
This template was designed to help developers showcase their skills and to help potential employers get a good idea of what they are looking for. The template makes it easy for developers to create a portfolio website without having to worry about design. The designs were made by a professional designer, so you can be sure that they will look great!
Portfolio Website Template – Personal Portfolio Website Free Download HTML CSS JavaScript
Case A: (b >= i && e <= j) If the current segment is entirely within i-j, the segment is relevant.
Case B: (i > e || j < b) In this case the current segment is entirely outside i-j, no need to take this segment.
Case C: If case A,B is not true, some part of this segment is between i-j, the segment should be further broken down and take the relevant part.
Then we go to each node in the query function to see if the segment is relevant or not. If it is relevant then we will return the sum of that node, if it is out then we will return 0, otherwise we will break the segment further and find the relevant part.
int query(int node, int b, int e, int i, int j)
{
if (i > e || j < b)
return 0; // has gone out
if (b >= i && e <= j)
return tree[node]; //relevant segment
int Left = node * 2; // More breaks to be done
int Right = node * 2 + 1;
int mid = (b + e) / 2;
int p1 = query(Left, b, mid, i, j);
int p2 = query(right, mid + 1, e, i, j);
return p1 + p2; //Sum of left and right sides
}
The query function works like the init function. i,j is the sum of the range to be extracted and b,e is the sum of the range in the current node.
Finally updated, for which I created the tree without using cumulative sum. You are told to change the index value of i=3 to x=10. That means I will update the node in the tree which has the sum of 3-3 range (yellow node in the image below). When the value of the node is updated, the sum of all the nodes that were in the path (blue nodes) will change, the rest of the nodes will not change because node number 3 is out of range.
There is not much difference in the updated code either:
void update(int node, int b, int e, int i, int newvalue)
{
if (i > e || i < b)
return; // has gone out
if (b >= i && e <= i) { //relevant segment
tree[node] = newvalue; // Set the new value
return;
}
int Left = node * 2; // More breaks to be done
int Right = node * 2 + 1;
int mid = (b + e) / 2;
update(left, b, mid, i, newvalue);
update(right, mid + 1, e, i, newvalue);
tree[node] = tree[Left] + tree[Right];
}
I will update the number index, I have omitted the extra segments at the beginning. When we go to the relevant segment, we put the new value, here the condition if(b==e) works even if we write it because we are always updating the leaf node.
Segment tree is roughly these 3 functions are always init,query,update. Sometimes the work of init can be done by updating. For example here you can create tree by updating each node separately without creating tree by calling init. Combining the 3 functions, the code would be:
#define mx 100001
int arr[mx];
int tree[mx * 3];
void init(int node, int b, int e)
{
if (b == e) {
tree[node] = arr[b];
return;
}
int Left = node * 2;
int Right = node * 2 + 1;
int mid = (b + e) / 2;
init(Left, b, mid);
init(right, mid + 1, e);
tree[node] = tree[Left] + tree[Right];
}
int query(int node, int b, int e, int i, int j)
{
if (i > e || j < b)
return 0; // has gone out
if (b >= i && e <= j)
return tree[node]; //relevant segment
int Left = node * 2; // More breaks to be done
int Right = node * 2 + 1;
int mid = (b + e) / 2;
int p1 = query(Left, b, mid, i, j);
int p2 = query(right, mid + 1, e, i, j);
return p1 + p2; //Sum of left and right sides
}
void update(int node, int b, int e, int i, int newvalue)
{
if (i > e || i < b)
return; // has gone out
if (b >= i && e <= i) { //relevant segment
tree[node] = newvalue;
return;
}
int Left = node * 2; // More breaks to be done
int Right = node * 2 + 1;
int mid = (b + e) / 2;
update(left, b, mid, i, newvalue);
update(right, mid + 1, e, i, newvalue);
tree[node] = tree[Left] + tree[Right];
}
int main()
{
READ(“in”);
int n;
cin >> n;
repl(i, n)
cin
>> arr[i];
init(1, 1, n);
update(1, 1, n, 2, 0);
cout << query(1, 1, n, 1, 3) << endl;
update(1, 1, n, 2, 2);
cout << query(1, 1, n, 2, 2) << endl;
return 0;
}
By repeatedly dividing the segment tree array into 2 parts, the depth of the tree will be at most log(n) so the complexity of each query and update is O(logn). The init function has to visit each node of the tree once so the complexity will be about O(nlogn).
Portfolio Website Template – Personal Portfolio Website Free Download HTML CSS JavaScript
You can use segment trees only when two smaller segments can be combined to produce a larger segment. In addition to the sum, you can find the maximum or minimum value in a range, if you know the maximum value on the left side and the maximum value on the right side, you can also find the root node very easily.
An important thing is missing here. Suppose you are not asked to update an index but asked to update from i to j index, then what to do? Updating each leaf node separately will reduce the complexity to O(nlogn) given by TLE. There is a very elegant technique for this called Lazy Propagation! I will know about that in the next episode, now solve the problem of array queries (lightoj), Multiple of 3 (SPOJ), Frequent Values (UVA), Curious Robin Hood (lighoj) with what you have learned.
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
All Links in Below:
Join Our FreeWebsiteCreate Facebook Group to get an instant update for projects, templates, design resources, and solutions.
Join Our YouTube Channel & Subscribe with Bell Icon for New Video:
Join Our Official Facebook Page For the Latest updates All Code Projects are Free:
Visit our service page to get premium services.
Free Website Create – HTML CSS, PHP, JavaScript Programming Projects For Free
Follow Us
Thank You,
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
FreeWebsiteCreate.net tries to provide HTML, CSS, SCSS, JavaScript, React, Android Studio, Java, PHP, Laravel, Python, Django, C#(C Sharp), and ASP.net-related projects 100% free. We try to make learning easier. Free Website Create always tries to give free projects to new learners. Free projects and source code will help to learn quickly.
They can save time and learn more. In this post, we share a free portfolio project website code with HTML and CSS. This free code portfolio contains a single landing page with a responsive design. In this post, we get a free best carpenter and craftsman service website designed by FreeWebsiteCreate with HTML, CSS, Bootstrap, and JavaScript.