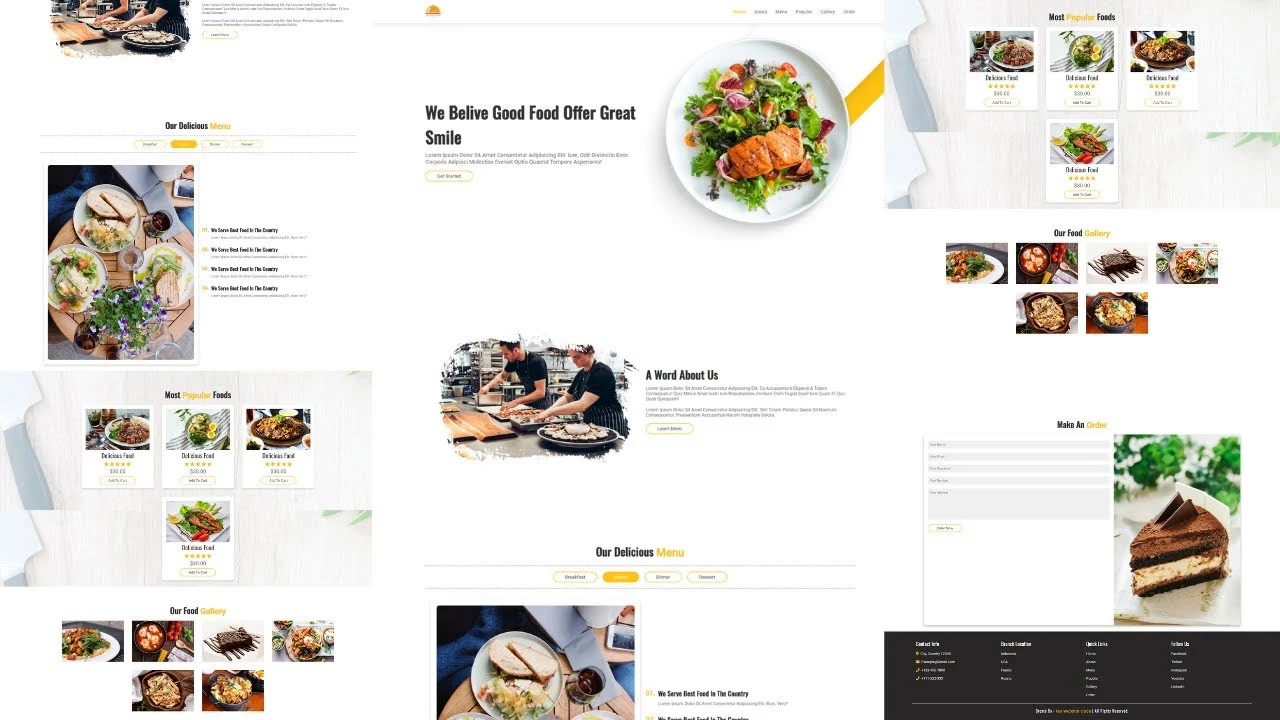
A Completely responsive food website template with HTML, CSS, Bootstrap, and JavaScript. This is also called a restaurant food website template design and you easily free download it from our website free website create. Food Website Design – Restaurant Website Design Free Download – Food Website – eCommerce Website Template
Food websites have exploded in popularity over the last few years with consumers searching for food information online. With this increase in popularity, the need for food websites has also increased. As a result, many food websites have been created with many different designs and themes. It can be hard to know what design to choose when creating a food website. In this post, I will show you the basic design of a food website, the design that I use for my food blog, and how you can create your own food website.
Food Website Design – Restaurant Website Design Free Download – Food Website – eCommerce Website Template
Data Structure: Segment Tree-1
You may have seen such problem in contest, given an integer array and many queries. Each query asks to sum all the numbers in a range. The size of the array is 10^5, the number of queries is also 10^5! You understand that you cannot find the sum by running a loop in each query. How to solve the problem?
It’s solution is very simple, you have to keep the cumulative sum. Suppose there is an array sum[MAX], then sum[i] contains the sum of all the numbers from index 1 to i. If sum from i to j is given(i<=j) sum[j]-sum[i-1] will be your answer. If you don’t understand, see the following example:
Input:
arr[]={4, -9, 3, 7, 1, 0, 2}
Calculate the cumulative sum:
sum[0]=0;
(for i=1;i<=n;i++) sum[i]=sum[i-1]+arr[i];
Then the cumulative sum will be:
sum[] ={4, -5, -2, 5, 6, 6, 8}
It’s child’s work, you can code it in 5 minutes. But the problem setter said to put you in danger the array will be changed every time you query!! Sometimes you will be asked to make the i-th index number x, and also the sum as before. What will you do now?
Now you will not work with cumulative sum, you will need a data structure called segment tree. You won’t be taught this in a data structure course at university, but it can be used to do a lot of work.
Before moving on to the next part you should be clear about a few things. If there is any ambiguity about recursion, it is best not to proceed. Also if you know about merge sort then understanding segmentation will be very easy for you. Also, if you don’t know anything about trees, is it okay to learn segment trees now? Just like Merge Sort, Segmentary Trio works in a “divide and conquer” manner.
The essence of the divide and conquer method is to break a problem into smaller parts, solve the smaller parts first, and derive the solution to the larger part from the solution of the smaller part. We will therefore split the array into 2 parts and calculate the sum of the two parts separately.
If you can find the sum of the left and right sides separately, you can easily find the sum of the larger part. Before I say it, you know what I’m going to do next. I will further fragment the smaller arrays until I get fragments of size 1. We know the sum of the pieces of size 1, from there we will find out the sum of the larger ones.
Although the picture may look strange, the thing is very simple. We break the array down into smaller ones, we know the sum of the smallest parts (leaf nodes), from there we can easily extract the larger ones by adding the left and right parts.
If we take each segment in the picture as a node, then a tree is created, each node has a part or the sum of the range. Its name is segment tree. Now you might be thinking how do you get the sum of parts i to j with this thing because we’re breaking the whole array and finally getting the sum of all of them. It will be answered shortly.
Notice that I have selected the previous tree tie but this time I have written only the range instead of showing the whole segments. For example, node number 3 contains the sum of all indices from 5 to 7. Node numbering is important. The root node will be 1, its left node will be 1*2=2, and its right node will be (1*2+1)=3. That is, if the root is x, the left side will be 2x and the right side will be 2x+1. This is a convenient way to store binary tree arrays.
Food Website Design – Restaurant Website Design Free Download – Food Website – eCommerce Website Template
Now let’s see how to create this structure. Look at the code below, the explanation is below the code:
#define mx 100001
int arr[mx];
int tree[mx * 3];
void init(int node, int b, int e)
{
if (b == e) {
tree[node] = arr[b];
return;
}
int Left = node * 2;
int Right = node * 2 + 1;
int mid = (b + e) / 2;
init(Left, b, mid);
init(right, mid + 1, e);
tree[node] = tree[Left] + tree[Right];
}
int main()
{
//READ(“in”);
int n;
cin >> n
repl(i, n) cin
>> arr[i];
init(1, 1, n);
return 0;
}
We will store the tree in the tree[] array. Size of tree array will be 3 times of input array (why??). The init function will create a tree from the arr array. The parameters of init are node,b,e, where node = current node and b,e are current range. Initially we will be at node 1 and in the range 1-7 (see the tree image).
If (b==e) then we have reached the last node, here the sum will be the value in the array, stored in the tree and returned. If (b==e) is not then the array must be divided into two parts. The index of the left side node will be node*2 and the right side will be node*2+1. And break the array right in the middle. Now if you call init recursively on both sides, the sum of the smaller parts on the left and right sides will be output. When both sides are done, the sum of the current nodes will be the sum of the left and right nodes.
If you have trouble understanding, simulate the code by hand once, only then it will be clear.
This time we need a query function that returns the sum of all the numbers between i and j.
For the range 2-6 the yellow nodes are our relevant nodes, the rest are extra. Our query function will only find the sum of the relevant nodes. The code will be similar to the init function but some conditions will need to be added. Suppose you are at a node where the sum of b-e ranges. How do you know if this node is relevant?
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
All Links in Below:
Join Our FreeWebsiteCreate Facebook Group to get an instant update for projects, templates, design resources, and solutions.
Join Our YouTube Channel & Subscribe with Bell Icon for New Video:
Join Our Official Facebook Page For the Latest updates All Code Projects are Free:
Visit our service page to get premium services.
Free Website Create – HTML CSS, PHP, JavaScript Programming Projects For Free
Follow Us
Thank You,
Before Download
You must Join our Facebook Group and Subscribe YouTube Channel
FreeWebsiteCreate.net tries to provide HTML, CSS, SCSS, JavaScript, React, Android Studio, Java, PHP, Laravel, Python, Django, C#(C Sharp), and ASP.net-related projects 100% free. We try to make learning easier. Free Website Create always tries to give free projects to new learners. Free projects and source code will help to learn quickly.
They can save time and learn more. In this post, we share a free portfolio project website code with HTML and CSS. This free code portfolio contains a single landing page with a responsive design. In this post, we get a free best carpenter and craftsman service website designed by FreeWebsiteCreate with HTML, CSS, Bootstrap, and JavaScript.